头部外伤仍然是全世界死亡和残疾的主要原因。虽然颅骨骨折是最常见的头部损伤之一,但颅骨的基本力学及其耐冲击能力仍不确定。在本研究中,我们提出了一种应变率相关的颅骨材料模型,并将其应用于特定对象的有限元(FE)头部模型中,以预测现实世界中五种跌倒事故中的颅骨骨折。受试者特定的头部模型是根据建立的基于图像注册的个性化流程开发的。利用个性化人体模型,通过事故重建得到头部碰撞边界条件。模拟的骨折线与每个受试者死后CT扫描中可见的骨折线进行了比较。结果表明,有限元模型确实预测了所有病例颅骨骨折的实际发生和程度。在至少五分之四的病例中,预测的骨折模式与CT扫描和尸检报告的结果相当。拉伸材料模型,从文献中调整为代表率相关的颅骨皮质拉伸数据,能够捕捉到在颅骨标本钝压痕加载中观察到的线性骨折。有限元模型对模型参数,特别是皮质表的本构参数非常敏感。尽管如此,本研究提供了目前缺乏的颅骨应变率相关材料模型,该模型具有准确预测线性骨折模式的能力。本文首次提出了一种利用计算工程技术重建颅骨骨折发生的程序,该程序捕获了所有骨折的起始、扩展和最终模式。
尽管过去几十年来在伤害预防方面取得了相当大的进步,但创伤性头部损伤仍然是全世界死亡和残疾的主要原因(福尔和科罗纳多,2015;Schmitt et al. 2019)。最常见的头部损伤之一是颅骨骨折(Malczyk et al. 2014),可能伴有其他严重损伤,如蛛网膜下、硬膜下或硬膜外出血(Aminoff et al. 2015)。颅骨骨折常见于跌倒、交通事故、袭击和谋杀的受害者(Motherway等人,2009),但其潜在的损伤机制很难阐明(Wilkins, 1997)。颅骨的基本力学仍在讨论中,这意味着尚未建立颅骨骨折的共识标准,这对于制定减轻头部损伤的干预策略至关重要(De Kegel et al. 2019)。阐明头部创伤损伤机制的困难也给法医病理学家带来了困境,他们通常面临着区分造成和意外原因的基本问题(Motherway et al. 2009)。
近年来,有限元(FE)模型已成为研究损伤机制和提出人类头部冲击容忍极限的有用预测工具(Giudice et al. 2019)。有限元模型作为人类头部的计算替代品,如果在使用之前进行适当的验证,它们可以真实地模拟动态加载响应(Kleiven 2006)。在FE头部模型的许多可能应用中,研究人员已经证明了FE工具在法医调查中的潜力。例如,Li等人(2019)使用特定于受试者的头部模型重建了疑似虐待婴儿的案件,并能够提供生物力学证据来支持法医评估。Kleiven(2006)在类似的范围内重建了一个涉及一名妇女遭受致命颅骨骨折的伤害案例。使用FE头部模型作为预测工具,Kleiven可以排除头部损伤的意外原因。在法医常规实践中利用FE重建有助于法医评估的客观化,避免了有时在法庭案件中出现的不同医学意见的风险(Wilkins 1997)。
对于上述应用,需要精确了解影响情景和人类主体,以及稳健可靠的数值模型。对有关生物组织的基本理解是必不可少的,因为有限元模型需要精确的材料配方。人类头骨可以看作是一个由两层致密的皮质骨和一层多孔的小梁骨(diplo?)组成的三层系统,它具有结构不均匀、粘弹性和复杂的微观结构安排。由于这一点,颅骨的建模失败已被证明是困难的。在实验研究中,输入材料参数的差异很大,这给颅骨骨折建模带来了进一步的障碍。diplo?和皮质骨的刚度和强度在受试者和颅骨位置之间有很大差异(Boruah et al. 2017;McElhaney et al. 1970)。颅层厚度(Auperrin et al. 2014),孔隙度/密度(Carter and Hayes 1976, 1977;Melvin et al. 1969)和受试者年龄(Auperrin et al. 2014;Sai et al. 2010)已被确定为影响颅骨基本力学特性的可能属性。最重要的是,许多研究人员已经指出形态变异是报道的材料参数广泛传播的关键因素之一(Zhai et al. 2020;Motherway等人,2009b;Rahmoun et al. 2014)。
颅骨的各种本构模型已经与FE头部模型一起提出,用于预测颅骨骨折(Barbosa et al. 2020;Ren et al. 2020;Cai et al. 2019;Ptak et al. 2018;Lozano-Mínguez et al. 2018;De Kegel et al. 2019;Haut and Wei 2017;Wang et al. 2014)。建议的颅骨材料模型通常包含各向同性线弹性或更简单的弹塑性公式,并结合脆性材料破坏规律。头部模型中的颅层通常在三层系统中以固定的厚度比例建模,并且没有受试者特定的头部几何形状。为了捕捉颅骨的孔隙度梯度,研究人员还致力于建立微结构启发模型(Weerasooriya and Alexander 2021;De Kegel et al. 2019)。最近,De Kegel等人(2019)将特定于受试者的材料应用于几何个性化的颅骨模型,以预测尸体实验中的颅骨骨折。在研究中,拉伸破坏极限和弹性模量与局部测量的骨矿物质密度有关。有限元重建成功地预测了复杂的颅骨骨折,显示了有限元模型的良好能力,但也显示了获得精确骨折模式的困难。
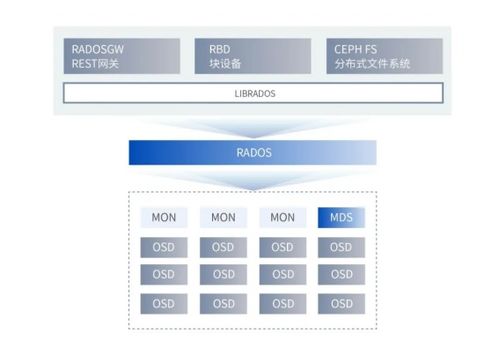
图1

研究概述。材料模型是通过先前发表的单轴拉伸和头骨压痕实验建立的,随后在宏观尺度的受试者特定头部模型中实施。碰撞运动学是基于使用几何个性化HBMs和法医记录的事故重建确定的。通过基于图像配准的个性化流程获得受试者特定的头部模型,并在最终模拟设置之前添加面部质量和头皮。最后,将模拟的断裂线与每个受试者的分段PMCT扫描进行比较,以评估材料模型在FE事故重建管道中预测观察到的断裂模式的能力
特定主题的材料模型非常耗时,并且需要一组复杂的数据,通常无法从标准的医院记录和医疗文件中获得。在一些研究中,在有限元模型中对骨骼和孔隙度的微观结构排列进行建模,结果表明模拟的预测能力只有很小的提高(Boruah et al. 2017)。尽管研究人员强调颅骨的粘弹性(Wood 1971;Boruah et al. 2013;翟等,2020;Motherway等人,2009b),很少有应变率相关的材料模型在FE头部模型中实现。文献中提出的大多数材料模型使用准静态压缩或拉伸试验得出的本构参数,即使模拟通常在动态加载条件下进行测试。
本文的目的是提出一种计算方法,通过建立颅骨应变率相关的材料模型来表征颅骨对冲击载荷的变形响应和骨折,并使用文献中的实验数据在两种不同的长度尺度上进行评估:皮质骨标本的单轴张力(Wood 1971)和颅骨钝压入载荷(Gunnarsson et al. 2021)。在建立材料模型的基础上,将特定受试者的头部有限元模型用于重建真实世界的坠落事故,以评估所提出的重建方法的预测能力。重建了5例法医坠落事故病例,并对颅骨模型进行了评估,以评估其预测这些病例观察到的颅骨骨折模式的能力。重建是用解剖学上详细的受试者特定的头部模型进行的,因此结合了头骨之间的形态学差异。使用计算工程技术重建颅骨骨折发生的程序被提议用于各种应用的准确颅骨骨折预测,并阐明FE作为循证医学中基于生物力学的工具的潜力。
研究范围概述如图1所示。本研究中涉及的所有模拟均在LS- prepost v4.8中进行预处理,在LS- DYNA v13 (LSTC, Livermore, CA, US)中进行多cpu模拟,并在MATLAB v2021a (The 251 MathWorks, Inc., Natick, Massachusetts, United States)中进行后处理。所有图像处理步骤,例如,头部尸检计算机断层扫描(PMCT)的分割和屏蔽,都是使用3D切片器v4.11完成的(开源软件可在www.slicer.org上获得)。
在本研究中,颅骨模型分为三层,包括外层和内部皮质层以及diplo?中间层。采用实心六面体网格单元对三层结构进行连续网格建模。所有颅层都被认为是结构各向同性和弹塑性的。由于颅骨的弹性模量和断裂应力随应变率的增加而增加(Wood 1971),因此在材料配方中考虑了应变率依赖性。假设内外皮质骨具有相同的材料特性,diplo?模型相似,只是降低了弹性模量和破坏阈值。本构模型旨在描述颅骨在动态加载事件中的力学行为,范围从小到高拉伸应变。
颅骨层用LS-DYNA库(MAT187)中的材料配方建模。该模型结合了应变率相关塑性和等效塑性应变相关破坏的公式。假定脆性破坏(无损伤演化),并对构件进行破坏后的侵蚀。材料的屈服面是用德鲁克-普拉格锥来描述的,破坏是用等效应变破坏准则来描述的。有关本构模型的更多细节,读者可参考原始出版物和LS-DYNA手册(Kolling and Haufe 2005;LST 2002)。
屈服应力作为拉伸和压缩塑性应变函数的表格曲线,以及杨氏模量作为有效应变率的函数作为输入。皮质表的输入数据是基于单轴拉伸实验得出的力学参数(Wood 1971)。弹性模量E [Pa]与应变速率[1/s]的关系式为
(1)
拉伸时的断裂应力[Pa]随应变速率[1/s]的增大而增大,关系如下:
(2)
注意,添加了因子6895以将原始方程的输出单位从lb/inch转换为Pascal。公式1和2来自Wood(1971)发表的对30具尸体头部的120个皮质骨标本的实验统计分析。
diplo?使用与皮质骨相同的材料模型进行描述,但刚度有所改变。Kohtanen等人(2021)通过对枕骨干骨段进行非接触振动实验,报道diplo?的弹性模量比皮质骨低60%。为了模拟diplo?,弹性模量(Eq. 1)因此相应地以0.40的因子进行缩放。对剪切模量进行了相同的缩放。关于diplo?的拉伸性能的报道很少,但准静态弹性模量符合人类股骨松质骨在拉伸状态下的报道范围(Carter et al. 1980)。同样,对于diplo?层准静态破坏应力,将破坏应力(Eq. 2)按0.10的系数进行缩放,以对应已报道的22个人类股骨样本的单轴准静态拉伸断裂应力的下端(Carter et al. 1980)。
假设颅骨各层的弹性模量在拉伸和压缩时相同。该假设基于实验结果(Oftadeh et al. 2015;罗宾斯和伍德1969)。指定了拉伸应变破坏准则,元件不允许在压缩中断裂。其他材料参数输入如表1所示。
表1头皮材料参数(Fahlstedt et al. 2015;Li et al. 2017)和头盖骨。骨密度为ba根据Kohtanen et al.(2021)报道的实验,皮质骨的剪切模量为ba基于Tang等人(2015)的工作。皮质骨与diplo?的泊松比为ba分别基于Peterson和Peterson and Dechow(2002)以及McElhaney等人(1970)的研究
2.1.1 e根据文献中的实验数据进行估值
根据Wood(1971)进行的单轴拉伸实验,对皮质骨的材料模型进行了评估。Wood从人尸体颅骨中提取狗骨状皮质骨,并对其进行准静态和动态加载。在本研究中,与Wood提出的尺寸相同的犬骨形券使用4000个六面体元素进行建模。元素大小与特定受试者头部模型中的网格元素大小相当(见第2.2.2节)。对试件一端施加位移,得到应变速率分别为0.1/s、10 /s和150/s。另一端采用固定的边界条件。试样一直受力,直到灾难性的破坏。模拟的应力-应变曲线最终与已发表的离体应力-应变曲线进行了比较(Wood 1971)。
头盖骨标本比传统头盖骨力学测试中常见的梁条、圆条或狗骨形标本大,但与全尺寸的尸体头部相比,它们可以进行更容易处理的实验,并捕获颅骨的多轴应力状态。为了证明本构模型的预测能力并可视化其断裂响应,模拟了头骨模型的钝压痕,步骤见图2。
模拟设置遵循Gunnarsson等人(2021)进行的实验。在实验研究中,从尸体头骨的上半部分切下圆顶状标本,不包括任何缝合线,外径在?75-150 mm之间。颅骨用?31.75毫米的半球形压头压痕,将标本撞击到外皮质骨上。压痕与内皮层表面的中心重合。样品自由地搁在金属板上。
在这项研究中,从一个特定受试者头部模型的顶骨中提取了一个头骨标本(稍后在第2.2.2节中介绍)。使用Hexotic软件对头骨进行了15万个实体六面体单元的网格划分。半长轴长度约为78毫米。以4.1 m/s的速度缩进颅骨,缩进时间为300 s。压头尖端和金属支撑板均为刚性模型,摩擦系数设为0.1。板在各个方向上受到约束,压头在与底支撑板相切的方向上受到限制。然后将失效模式、断裂线以及力-位移响应与离体观察结果进行比较(Gunnarsson et al. 2021)。
图2

Gunnarsson等人(2021)实验的颅骨钝压痕模拟
表2 Des案例和主题的描述。受试者的年龄、身高和体重不予披露,以保持受试者的完整性
从哥本哈根大学法医学部门尸检的死者数据库中选择了五个真实的坠落法医案例(命名为案例1至案例5)(Henningsen et al. 2022)。所有受试者都遭受钝力颅骨创伤,每个人都有头部的死后计算机断层扫描(PMCT)记录。一名经验丰富的法医病理学家和一名初级医生描述了事故发生的过程,并追踪了撞击点。结论是根据警方和尸检报告、医院记录和PMCT得出的。PMCT被分割,不包括面部骨和面部软组织。头皮、外、内皮质骨、diplo?用掩膜分层分离。通过ct值(Hounsfield Unit)分割diplo?和皮质骨。整个颅骨厚度构成了一个单一的分割。在该分割中,随后使用3D切片器中的“阈值工具”对下HU diplo?进行分割,并设置为覆盖皮质骨分割(整个颅骨厚度的分割)。将头皮合并为致密结缔组织头皮和软组织头皮的单层。遮罩是使用3D切片器中的半自动方法创建的(Fedorov等人,2012)。
这五宗法医案件分别是站立坠落、高处坠落或低速交通事故。四个法医案例涉及向后跌倒,冲击枕骨。一个案例涉及从高处坠落,导致额骨撞击。表2列出了法医案件的详细情况。在病例1至病例4中,受试者在枕骨处出现颅骨线状骨折,而在病例5中,受试者在额骨处出现圆形骨折,线状骨折向下辐射并延伸至眶顶。脸部的中下部是先着地还是先着地并不明显。
2.2.1 事故重建使用HBMs的指令
为了获得坠落事故的头部撞击速度,使用几何个性化人体模型(HBMs)重建了所有五个病例(见图4)。将SAFER THUMS HBM v10 (Pipkorn et al. 2022)的直立第50百分位行人版本作为基线HBM,随后对其进行非线性变形以匹配受试者的人体测量。HBMs的外表面(皮肤)被变形成与病例受试者具有相同身高、年龄和体重指数(BMI)的站立男性或女性参考几何形状。参考几何图形来自开源,最初是从高分辨率激光扫描和人体测量数据的统计分析中开发出来的(Humanshape.org, 2022)。调整HBM软组织的密度以获得病例受试者的正确质量。变形过程遵循Li(2021)提出的相同基本步骤。读者可参考原始出版物了解更多细节。
图3

头部模型装配与颅骨及其层的切片和详细视图
图4

病例1至5的个性化HBMs(从左至右)
大致位置、方向和腿/手臂位置是根据法医评估得出的。hbm使用牵线木偶方法定位,部分由Poulard等人(2015)描述,其中应用节点对之间的电缆将模型移动到所需位置。缆索(以梁单元的形式表述)被定义为强制运动的初始拉力,并且在模拟过程中使用位移阻尼器来帮助模型沉降。对于病例2,左肘的位置是为了支撑向后摔倒。病例5,右臂位于HBM胸部前方。
为了重建病例1、3和4,hbm在初始倾斜和施加重力载荷的情况下定位。不施加初速度。膝关节被锁定以减少自由度,避免不一致的结果。
对于案例2的重建,将一个类似自行车车把的圆柱体建模为冲击器。圆柱体的初始速度为25 km/h,持续30 ms,正面撞击腹部的HBM。HBM没有初始倾斜度和速度,也没有关节锁定。
对于案例5,HBM在施加重力载荷的情况下几乎水平放置在140厘米的高度。最初的倾斜是为了确保HBM俯卧着地,膝盖落在较低的楼梯台阶上。增加了一个额外的地面表面,以模仿小腿撞击的较低的楼梯台阶。
模拟后,提取头部碰撞前时间步长的头部速度(从头部重心处),并将其作为特定受试者FE头部模拟的边界条件。
2.2.2 头部撞击记录仪使用特定受试者头部模型进行教学
从HBM模拟中获得的边界条件,即头部撞击速度,应用于受试者特定的头部模型,以预测各自的颅骨骨折。头部模型被放置在法医调查得出的撞击点上。与HBM头部相比,受试者特异性头部模型使用足够精细的网格构建,以区分骨折线,并且与一般HBM头部模型相比具有更多的解剖细节。
受试者特定头部模型是在基线头部模型(ADAPT)的基础上开发的(Li et al. 2021;Li 2021),其中包括脑、脑膜、脑脊液、上矢状窦和颅骨。ADAPT模型的颅骨分为内皮质骨、多孔diplo?和外皮质骨,如图3所示。该模型采用约400万六面体单元和50万四面体单元的连续网格进行网格划分。元件尺寸从0.50 mm到2.50 mm不等。用脑-颅骨相对运动、脑应变和颅内压的实验数据对模型进行了评价。ADAPT模型及其diplo?-cortical骨比最初是基于对152名健康成人受试者的MRI扫描生成的通用ICBM152模板的重建而开发的(Fonov et al. 2009)。
根据Li(2021)建立的基于图像配准的个性化流程,对每个案例的基线ADAPT模型进行了变形。该方法包括图像配准、网格变形和网格分组。PMCT扫描被分割成头皮、颅骨和头盖骨。然后将分割严格对齐到ADAPT头部模型。分割后的PMCT扫描和对应的蒙版分别来自五个受试者,作为模板,或所谓的固定图像,用于变形过程。通过图像配准获得位移场,并将ADAPT变形为五个受试者特定的头部模型,捕获受试者的头骨几何形状。变形是使用3D切片器模块BRAINSdemonWarp中实现的恶魔注册算法完成的(Johnson and Zhao 2009)。使用所提出的方法,FE颅骨的厚度,几何形状和大小保持真实的受试者的PMCT。随着颅骨内外表面的变形,原始的diplo?-cortical骨厚比根据所施加的位移场进行变换。在一些地区,diplo?更广为人知,而在其他地区则几乎不存在。这里只提供了变形过程和头部模型的简要概述;先前已记录了更多细节(Li et al. 2021;李2021年)。
为了量化个性化的准确性,我们计算了Dice分数。Dice是测量受试者特定头部模型和PMCT扫描之间的空间重叠(Ou et al. 2014)。5个个性化头像模型的Dice平均得分均>0.80。Dice值为0表示PMCT分段表面与变形表面没有重叠,而Dice值为1表示完全重叠。每个受试者特定头部模型的最小雅可比值在0.120.31之间。
由于ADAPT头部模型不包括头皮,因此在模型中加入局部应用的头皮斑块,覆盖颅骨的冲击区域。头皮分为两层,一层代表真皮层,第二层代表头皮的两层脂肪层和中间的盔状膜腱膜。两层均采用一阶Ogden增生模型(LS-DYNA文库中的*MAT077O)建模,参数见表1。头皮均匀厚,颅骨外表面法向有六层实性元素,如图3所示。每位受试者的头皮厚度是根据在撞击部位的CT扫描测量得出的。通过使用局部涂抹的头皮而不是覆盖整个头骨的头皮,ADAPT模型节省了多达一百万个元素。头皮与冲击材料之间的摩擦系数假设为0.40,这在报道的人类皮肤范围内(Derler and Gerhardt 2012)。
额外的淋巴结肿块均匀分布到覆盖FE头部模型眶顶和颅底的节点集中,以弥补缺失的面部肿块。加上面部组织和面部骨骼,头部的总重量估计为4.03 kg (Yoganandan et al. 2009)。因此,增加的质量等于4.03 kg与没有集总质量单元的有限元模型的质量之差。
所有情况下的冲击材料都假定是相对刚性的,与瓷砖、沥青、混凝土和硬填料土一致。弹着点表面为线弹性材料,弹性模量为10 GPa,泊松比为0.25,密度为2700 kg/m。
穿透厚度的骨折线被推断为在所有三个颅骨层中网格元素被侵蚀的区域。模拟持续时间为6.0 ms,覆盖了整个撞击事件。
摘要
1 介绍
2 材料与方法
3.结果
4 讨论
5 有限公司
结论和未来的工作
数据可用性
代码的可用性
参考文献
致谢
作者信息
道德声明
附录A
搜索
导航
#####
图5

试验(Wood 1971))和模拟应力-应变曲线,用于犬骨形皮质骨试样在三种应变率下的拉伸直至失效。破坏后,构件中的应力等于零。添加diplo?的拉力试验以供参考
图6

实验(Gunnarsson et al. 2021)和模拟力施加于头骨样本,说明了灾难性破坏之前的断裂开始和扩展。从上面看标本,观察外皮质骨。撞击点以红色标示
图5为犬骨形试件在三种不同应变速率下的单轴拉伸实验(Wood 1971)和模拟应力-应变曲线。在垂直于试样中部加载的方向上,单个断裂开始,并迅速导致中部区域所有元素的破坏。中截面上各单元均被侵蚀,未发生缩颈。
图6给出了颅骨模拟中压头的实验(Gunnarsson et al. 2021)和模拟力-时间历史,并给出了断裂扩展的图解时间轴。第一次裂缝开始于内皮质表的中心,并向头骨边缘扩展到diplo?和外皮质表。裂纹从帽檐边缘扩展为一个贯穿厚度的裂纹,并向中心区域的撞击点扩展。在到达冲击区之前,试样边缘产生了贯穿厚度的二次裂纹。它以与最初裂缝相同的方式向撞击点移动。最终的灾难性破坏发生在两个裂纹在冲击区域相交时。最后,出现了两个较小的裂缝。其中一个裂纹起源于撞击区并向外辐射,第三个裂纹是在第一个裂纹的相反边缘产生的。颅骨模拟中的载荷为压头在载荷方向上的反力,最大载荷为4540 n,达到峰值后发生宏观断裂。
使用个性化HBMs重建病例的下降序列如图7所示。注意,情况1和4与情况3具有几乎相同的下降时间历史。获得的头部撞击速度,以及测量的头皮厚度和应用的面部质量,如表3所示。水头速度按分量表示:横向的速度分量和垂直于地面的速度分量。
表3测量每个受试者的头皮厚度和增加的面部质量,以及使用几何人物推导的应用头部撞击速度nalized hbm。[2列拟合表]
图7

以选择的时间步长绘制重建的坠落事故的坠落序列。注意,情况1和4与情况3具有几乎相同的下降时间历史
图8

重建病例1至5的最终骨折模式。模拟中的初始头部位置用箭头表示,以指示合成速度方向。已证实的撞击位置用红色突出显示,断裂线用黑色表示。请注意,病例5的受试者经历了开颅手术,因此可以看到一些额外的线条。切开术和分割伪影不能与黑色撞击造成的骨折线混淆。实际骨折线的可视化也受到部分愈合的影响。病例2至4为后视图,病例1为后险恶视图,病例5为前视图
图9

五种模拟变化的敏感性研究。病例2分别模拟一次diplo?和皮质骨较弱,一次没有头皮,一次头部质量较轻,一次正常头部撞击速度较低和较高
最终颅骨骨折见图8。在所有的模拟中,断裂都是在远离撞击区域的距离开始的,并且几乎是瞬间向撞击点方向和/或远离撞击点方向传播的。所有可见的裂缝线均为透厚裂缝。每一个贯穿厚度的断裂都是由内部皮质表的侵蚀元素开始的。
在病例1中,模拟骨折沿着通往枕骨大孔的路径,与PMCT中所见相似。通过有限元模拟,预测骨折线不会朝上前方的小羔羊骨缝合方向运行。
在病例2中,预测发生前后连续性线性骨折。骨折线延伸至枕骨大孔,类似于PMCT的骨折。
病例3预测为t型骨折,垂直腿向枕骨大孔方向延伸。在PMCT中没有观察到水平腿,但线状骨折的位置和性质是相似的。PMCT骨折遵循比有限元预测更弯曲的路径。有限元模型进一步预测骨折通过枕骨大孔扩展到蝶骨。在PMCT中未见此类骨折延伸。
在病例4中,在PMCT中看到的实际骨折从枕骨的撞击部位向下延伸到枕骨大孔。模拟预测骨折在顶骨向前发展。
在病例5中,有限元模拟高估了PMCT中出现的颅骨骨折模式。在有限元模型中,发现初始骨折靠近眶缘,并向撞击点延伸。最终的裂纹模式由几条从撞击点向外辐射的断裂线和一条与地面接触区域同心的环绕断裂线组成。病例5显示了初始和最终粉碎性骨折模式(图8)。菱形骨折与延伸至左眼眶和前窝的线状骨折的相似之处可以区分出来。
在修正的模拟条件下,对Case 2进行了敏感性分析。调查了以下情况:
1.
将diplo?极限拉伸应变降低0.001,从而降低diplo?强度(见附录)。
2.
通过将皮质骨极限拉伸应变降低0.001来降低皮质强度(见附录)。
3.
头皮完全切除
4.
减少了0.50公斤的头部质量
5.
降低冲击法向速度0.50米/秒
6.
增加冲击法向速度0.50米/秒
从试验(a)到(f)得到的断裂线如图9所示。降低diplo?破坏应变后,断裂线的大小不变。病例2由于皮质骨强度降低,骨折变得更加严重。同样,通过移除头皮,从明显的中心区域放射出额外的线状骨折。有限元模型还预测了一个被裂缝的辐射臂拦截的同心裂缝。通过将头部质量和撞击速度分别降低0.50 kg和0.50 m/s,撞击没有导致任何贯穿厚度的断裂线。在头质量降低的模拟中,观察到内皮质表的线性骨折线(类似于参考骨折线)。将法向速度增加0.50 m/s,也会增大断裂的严重程度。附加的研究参数灵敏度见附录。
本研究提供了目前缺乏的颅骨应变率相关材料模型,该模型具有准确预测线性骨折模式的能力。线状颅骨骨折是最常见的骨折类型(Asirdizer et al. 2021;Whitwell et al. 2021),被认为是由撞击位置一定距离处头盖骨向外弯曲引起的拉伸应力引起的(Gurdjian et al. 1949)。由外弯曲引发的线性骨折通常延伸至撞击点,也向相反方向延伸至结构薄弱区域,如颅底(Whitwell et al. 2021)。本文提出了一种新的方法来重建颅骨骨折的发生,利用计算工程技术捕捉所有骨折的发生、扩展和最终模式。
该模型已被证明可以再现皮质骨在张力下的力学响应,同时正确捕获颅骨标本钝压痕加载的失效机制。本研究中计算得到的应力-应变曲线与皮质骨的实验结果一致(Wood 1971)。在离体实验中,皮质骨标本均在近似垂直于长轴的平面上失效。与此一致的是,在模拟拉伸试验中观察到垂直突变断裂。
在模拟人头帽钝压痕加载中,人头帽断裂成两部分。两个贯穿厚度的线状裂缝在帽檐边缘开始,并向加载点扩展。相交的断裂线几乎相互垂直,形成一个近似圆形的扇形(见图6)。这与相应的实验(Gunnarsson et al. 2021)有明显的相似之处,该实验结合了两个进行的高速率体外加载实验。在第一次试验中(冲击速度为4.1 m/s),试样被加载,直到穿透厚度裂缝将头骨裂成两部分。第二阶段(冲击速度为3.8 m/s),试样在宏观断裂开始前卸载。两个试样的主要宏观断裂起裂位置都在试样边缘,这与本研究的计算机模拟结果一致。在第一个离体试样中,初始边缘断裂随后通过加载点扩展。第二个宏观裂缝在撞击点开始,并向边缘扩展,导致裂缝线几乎垂直于第一个裂缝线。两条线性裂缝在加载点相交,沿一个方向向边缘辐射,将帽板切割成两部分(一个圆形扇形和一个圆形扇形),类似于图6所示的硅灾难性破坏。
在硅壳加载试验中,在突变破坏前产生了两个边缘裂纹。因此,在第二个离体试样中观察到两个边缘微断裂,其加载点与边缘距离约为三分之一。在第二次离体实验中,在宏观断裂开始之前,在加载点正下方观察到一个小的微断裂,如图所示。Gunnarsson等(2021)也在加载点或加载点附近观察到了内工作台的微破裂起裂。在模拟宏观断裂之前,记录了内工作台的微断裂。内台面的微骨折是在撞击点下方开始的。
钝压痕加载实验中观察到的峰值力在硅模型中为4.5 kN,在体内为4.0 kN,表明硅模型的刚度被高估了。骨折线和峰值力的差异可归因于颅骨形态的差异。用于实验和模拟的头骨帽并非取自相同的头骨标本,因此具有不一致的diplo?-cortical骨率,形状和大小。如前所述,形态变化通常被认为是实验中力学变化的关键因素(Zhai et al. 2020;Motherway等人,2009b;Rahmoun et al. 2014)。无论如何,与实验相比,该模型具有较好的破坏模式预测能力:在宏观断裂开始之前,硅头骨确实经历了载荷的增加,然后是短暂的软化和载荷平台。
单纯向后跌落病例(病例1、病例3和病例4)的头部撞击速度变化不大。三种情况下的法向速度分量在5.46 ~ 5.63 m/s之间。Hamel等人(2013)使用根据三种身体高度(160、170和180厘米)和两种身体质量(50和75公斤)组合缩放的身体模型,对可比较的向后跌倒进行了刚体模拟。在本研究中,身体被施加一个初始倾斜度,没有初始速度。对关节进行了两次模拟,一次为锁定关节,一次为未锁定关节。与本研究不一致的是,Hamel等人认为受试者之间的差异更大:观察到头部撞击速度随受试者身高和体重的增加而增加。然而,在所有情况下,头部撞击速度在3.715.02 m/s(锁定关节)和4.626.15 m/s(自由关节)之间。本研究中使用FE HBMs报道的撞击速度接近报道的范围。值得注意的是,其他头部撞击速度已经报告使用测试假人。Hajiaghamemar等人(Hajiaghamemar等人,2015年)报告了使用第50百分位男性测试假人观察向后跌倒时较低的头部撞击速度。在有髋部弯曲和没有髋部弯曲的情况下,跌倒的平动头部撞击速度分别为4.85 m/s和6.75 m/s。
有限元模型确实预测了所有病例颅骨骨折的实际发生和程度。然而,预测的骨折模式与PMCT扫描中看到的骨折有不同程度的一致性。
在病例4中,有限元模型表明,坠落导致从枕骨撞击部位向前推进的线性颅骨骨折。在PMCT中看到的实际骨折从枕骨的撞击部位向下延伸到枕骨大孔。模拟与pmct的差异有几种可能的解释。有些可能在于头骨的形态,有些可能在于所作的假设和简化。这个特殊的案例将在附录中进一步讨论。无论如何,应该强调的是,即使骨折与现实世界的骨折不对应,FE头部模型实际上确实准确地预测了线性颅骨骨折的实际发生。因此,病例4的模拟为可能的损伤模式提供了有价值的信息,尽管骨折的扩展可能值得怀疑。由于在之前发表的骨折预测尝试中没有考虑颅骨骨折的传播和开始,因此本研究的结果特别值得注意。案例4还强调了模型对输入参数的敏感程度。De Kegel等人(2019)在另一项使用特定受试者的有限元模型预测实验性颅骨骨折模式的尝试中也强调了同样的观点。作者对应用程序的有限元模型的鲁棒性表示关注,因为他们观察到对建模参数(例如,撞击点和几何形状)相当敏感。
病例5的有限元模型高估了额骨骨折。在这种情况下,高估的断裂可能伴随着高估的冲击速度。一般来说,我们可以假设骨折越严重,冲击力越大,并且随着冲击力的增加,在二次或第三次应力区会出现额外的线性骨折(Whitwell et al. 2021)。在这五起事故中,案例5与最多的未知参数相关。首先,尽管进行了广泛的法医调查,但最初的撞击点,无论是脸部还是前额,都没有得出结论。其次,受试者摔倒时右臂在胸前,导致肱骨骨折。目前尚不清楚受试者在多大程度上支撑着坠落,而手臂可能比HBM模拟显示的更能抑制坠落。在没有肌肉激活的情况下,使用HBMs捕捉这些事件是具有挑战性的。换句话说,案例5的头部撞击速度包含一定程度的不确定性。灵敏度研究表明,该模型对实际冲击速度非常敏感。
病例3准确预测枕骨骨折。然而,模拟骨折线继续穿过枕骨大孔(脊髓穿过枕骨的入口点)并延伸到前窝。虽然枕骨骨折延伸至后窝和前窝并不罕见(Whitwell et al. 2021),但在PMCT中未观察到基底骨折。对骨折线预测过高的解释可能在颅骨网格人工制品中找到。Dice值在枕骨大孔周围区域最低。也就是说,与头部的其他部分相比,模型的几何形状在那个特定区域是最不准确的。同时,枕骨大孔边缘的网状结构相对尖锐,呈锯齿状。这种突然的几何变化可能导致应力集中,这可能导致骨折线错误地穿过枕骨大孔,如病例3所示。
diplo?在动态载荷下的拉伸性能不像皮质骨那样被广泛报道,因此,在整个研究中进行了建模简化。一个值得注意的假设是diplo?在颅骨的机械反应中不太重要的作用。diplo?被认为仅仅是将机械载荷从皮质外表面转移到内部,而不像皮质表被认为具有主要的承载功能。与皮质骨相比,diplo?对颅骨结构完整性的影响较小,这一前提是基于Wood(1971)的基本理论和相关实验发现(Zhai et al. 2020;Melvin et al. 1969)。在此假设下,diplo?在本构建模中被忽略。从本质上讲,diplo?被认为就像皮质骨一样,只是在弹性模量和极限抗拉强度方面较弱。实际上,diplo?在力学意义上与皮质骨有很大的不同。为了支持所做的假设,用diplo?的较低抗拉强度和皮质骨的较低抗拉强度分别模拟了一次病例2。通过与原始病例2模拟的比较,diplo?抗拉强度的降低对最终颅骨骨折的影响可以忽略不计。另一方面,皮质强度的降低对预测骨折有明显的影响。敏感性分析强化了皮质骨本构建模比diplo?在当前应用中更为重要的假设。当然,diplo?的力学行为不应完全忽略,而应作为未来研究的目标。
本研究的重点是颅骨的拉伸破坏,而压缩破坏在某种程度上被忽视了。这种方法的基本原理是,线性撞击诱发的颅骨骨折很可能是由撞击部位附近颅骨的拉伸应力引起的(Wood 1971;Melvin et al. 1969)。此外,已知骨对压缩力比拉伸力具有更大的耐受性(Whitwell等,2021),皮质骨的压缩破坏强度大大高于拉伸破坏强度(Cezayirlioglu等,1985;Yeni et al. 2004)。因此可以认为,在本研究中提出的钝力创伤中,骨的拉伸特性比压缩特性更相关。在之前的研究中已经采用了这种方法,并且排除压缩破坏已被证明是获得线性断裂模式的成功策略(De Kegel et al. 2019)。
本研究中提出的颅骨的一般材料模型包括了进一步的简化,可以在未来的研究中考虑。首先,在本研究中,内外皮质骨的材料参数是相同的,尽管研究人员认为两层的刚度不同。Peterson和Dechow(2002)用超声波测定了人类顶叶皮层的弹性特性,认为顶叶皮层的外表比内表更硬。皮质骨也具有各向异性,这与McElhaney等人(1970)和Wood(1971)主张的切向各向同性的结果相矛盾。其次,众多研究表明力学参数的区域差异(Boruah et al. 2017;McElhaney et al. 1970;Kohtanen et al. 2021)在本研究中未被考虑。应该提到的是,一些研究人员也声称没有区域差异(Wood 1971)。第三,所提出的模型没有考虑受试者的年龄,而年龄也被认为是力学参数的决定因素(Auperrin et al. 2014;Sai et al. 2010)。Wood(1971)在这里也没有发现皮质骨在单轴拉伸下的断裂应力或应变有任何年龄依赖性,弹性模量的年龄依赖性非常小。最后,人类颅骨通过纤维关节(缝合线)相互连接。本研究未考虑颅骨缝合,其对骨折类型的影响有待进一步研究。
所提出的模型有几个优点。首先,材料公式相对于其良好的预测能力而言是异常通用的。最近,在文献中已经看到了特定主题的材料模型(De Kegel et al. 2019;Weerasooriya and Alexander 2021)。这些类型的模型需要大量的预处理和计算时间,并且与非特定主题模型相比,裂缝可预测性的改善微乎其微(Boruah et al. 2017)。本研究建议的颅骨材料模型需要有限数量的独立材料特性,并展示了利用通用材料配方的潜力。其次,通过实施剪切实验数据和更广泛的应变率选择,或LS-DYNA库中提供的材料配方*MAT187支持的其他输入,可以很容易地进一步推进所提出的材料模型。断裂应力和弹性模量的主题和区域特定调整可能会改善模型的预测结果。
提出了一种利用计算工程技术重建颅骨骨折发生的新方法,以捕获所有骨折的起始,扩展和最终模式。颅骨的同位素,应变率依赖和弹塑性材料模型已经提出并在一组选定的应用评估。该模型已被证明可以再现皮质骨在张力下的力学响应,同时正确捕获颅骨标本钝压痕加载下线性骨折的失效机制。该模型在宏观尺度上通过使用受试者特定头部模型重建五起坠落事故进行了测试。线性骨折模式的预测与大多数病例的PMCT扫描和法医分析一致。该模型对头部质量分布、冲击速度和皮质骨本构变量具有较高的敏感性。所提出的重建颅骨骨折发生的程序可用于在线性骨折占主导地位的各种应用中进行颅骨骨折预测。
作为这项研究的继续,还应研究该模型在高/低速度范围内预测更复杂骨折模式的能力,以及其他骨折模式(例如凹陷性骨折)和更广泛年龄组的预测能力。最重要的是,应该评估模型的通过/失败(断裂/无断裂)预测能力。在本组病例中,没有骨折介入缝合。然而,对于未来的研究,探讨颅缝的作用可能是相关的。添加剪切表格曲线或受试者特定参数也可能是研究范围。经过进一步验证,该方法可用于制定颅骨骨折标准,并有可能帮助法医病理学家推断颅骨骨折的原因。
下载原文档:https://link.springer.com/content/pdf/10.1007/s10237-023-01768-5.pdf